Skip to contents

infiltration

Source: R/RcppExports.R
infilt.Rd

In hydrological modeling, infiltration refers to the process by which water from precipitation snowmelt or irrigation enters the soil (Maidment 1993) .

Under the concept of the conceptual HM, the flux of infiltration is always calculated by the amount of water on the land \(W_{land}\), which can be precipitation, precipitation after interception, or precipitation with snowmelt, among others. The second point to consider is the water acceptability of the soil layer (\(C_{soil} - W_{soil}\)).

So we can give the function from:

\[F_{iflt} = f_{infilt}(D_{land}, D_{soil})\]

to:

\[F_{iflt} = f_{infilt}(W_{land}, W_{soil}, C_{soil}, ...)\]

some methods will tread the infiltartion as the part of th pounded water so there is also:

\[F_{iflt} = k^* W_{land}\]

where

  • \(F_{iflt}\) is infilt_mm

  • \(W_{land}\) is land_water_mm

  • \(W_{soil}\) is soil_water_mm

  • \(C_{soil}\) is soil_capacity_mm

  • \(k^*\) is estimated ratio.

The output density distribution from 9 methods:

Usage

infilt_GR4J(land_water_mm, soil_water_mm, soil_capacity_mm)

infilt_UBC(
  land_water_mm,
  land_impermeableFrac_1,
  soil_water_mm,
  soil_capacity_mm,
  param_infilt_ubc_P0AGEN
)

infilt_SupplyRatio(
  land_water_mm,
  soil_water_mm,
  soil_capacity_mm,
  param_infilt_sur_k
)

infilt_AcceptRatio(
  land_water_mm,
  soil_water_mm,
  soil_capacity_mm,
  param_infilt_acr_k
)

infilt_SupplyPow(
  land_water_mm,
  soil_water_mm,
  soil_capacity_mm,
  param_infilt_sup_k,
  param_infilt_sup_gamma
)

infilt_AcceptPow(
  land_water_mm,
  soil_water_mm,
  soil_capacity_mm,
  param_infilt_acp_k,
  param_infilt_acp_gamma
)

infilt_HBV(
  land_water_mm,
  soil_water_mm,
  soil_capacity_mm,
  param_infilt_hbv_beta
)

infilt_XAJ(land_water_mm, soil_water_mm, soil_capacity_mm, param_infilt_xaj_B)

infilt_VIC(land_water_mm, soil_water_mm, soil_capacity_mm, param_infilt_vic_B)

Arguments

land_water_mm

(mm/m2) pounded water volume in landLy and there is no limit, different than land_interceptWater_mm

soil_water_mm

(mm/m2) water volume in soilLy

soil_capacity_mm

(mm/m2) average soil Capacity (maximal storage capacity)

land_impermeableFrac_1

<0, 1> the maximum impermeable fraction when th soil is fully saturated

param_infilt_ubc_P0AGEN

<0.1, 4> coefficient parameter for infilt_UBC()

param_infilt_sur_k

<0.01, 1> coefficient parameter for infilt_SupplyRatio()

param_infilt_acr_k

<0.01, 1> coefficient parameter for infilt_AcceptRatio()

param_infilt_sup_k

<0.01, 1> coefficient parameter for infilt_SupplyPow()

param_infilt_sup_gamma

<0, 1> parameters for infilt_SupplyPow()

param_infilt_acp_k

<0.01, 1> coefficient parameter for infilt_AcceptPow()

param_infilt_acp_gamma

<0.001, 5> parameters for infilt_AcceptPow()

param_infilt_hbv_beta

<0.001, 5> parameters for infilt_HBV()

param_infilt_xaj_B

<0.01, 3> parameters for infilt_XAJ()

param_infilt_vic_B

<0.01, 3> parameters for infilt_VIC()

Value

flux of infiltration from land surface to soil layer

infilt_mm (mm/m2)

_GR4J (Perrin et al. 2003) :

\[F_{iflt}=\frac{C_{soil}\left(1-\left(\frac{W_{soil}}{C_{soil}}\right)^{2}\right) \tanh \left(\frac{W_{land}}{C_{soil}}\right)}{1+\frac{W_{soil}}{C_{soil}} \tanh \left(\frac{W_{land}}{C_{soil}}\right)}\]

_UBC (Quick and Pipes 1977) :

estimate the ratio \(k^*\) as: \[k^* = p_{imper} 10^{\frac{W_{soil}-C_{soil}}{p_{AGEN}}}\] where

  • \(p_{imper}\) is land_impermeableFrac_1

  • \(p_{AGEN}\) is param_infilt_ubc_P0AGEN

_SupplyRatio:

is a very simple method, which estimate only the pounded water: \[k^* = k\] where

  • \(k\) is param_infilt_sur_k

_AcceptRatio:

\[F_{iflt} = k (C_{soil} - W_{soil})\] where

  • \(k\) is param_infilt_acr_k

_SupplyPow:

is a very simple method, which estimate only the pounded water: \[F_{iflt} = kW_{land}^{\gamma}\] where

  • \(k\) is param_infilt_sup_k

  • \(\gamma\) is param_infilt_sup_gamma

_AcceptPow:

\[F_{iflt} = k \left(\frac{C_{soil} - W_{soil}}{C_{soil}} \right)^{\gamma}\] where

  • \(k\) is param_infilt_acp_k

  • \(\gamma\) is param_infilt_acp_gamma

_HBV (Lindstroem et al. 1997) :

estimate the ratio \(k^*\) as: \[k^* = 1-\left(\frac{W_{soil}}{C_{soil}}\right)^{\beta}\] where

  • \(\beta\) is param_infilt_hbv_beta

_XAJ (Zhao 1992) :

\[F_{iflt} = MM \frac{\left( \frac{MM - AU}{MM} \right)^{B+1} - \left( \frac{MM - AU - W_{land}}{MM} \right)^{B+1}}{B+1}\] \[AU = MM - \left( \frac{(1 - W_{soil})(B+1)}{MM} \right)^{1 / B - 1} \] \[MM = C_{soil}(B+1) \] where

  • \(B\) is param_infilt_xaj_B

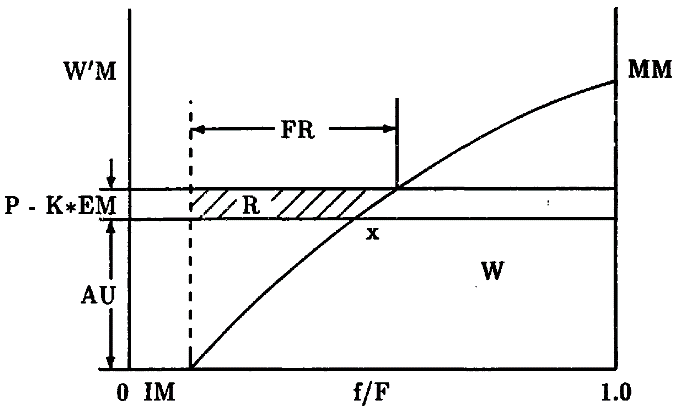
_VIC (Wood et al. 1992) :

\[F_{infilt} = \int_{i_{0}}^{i_{0}+P} A(i) {\rm d} i\] \[i = C_{soil}(B+1) \left[ 1 - (1-A)^{1/B} \right]\] where

  • \(B\) is param_infilt_vic_B

References

Lindstroem G, Johansson B, Persson M, Gardelin M, Bergstroem S (1997). “Development and Test of the Distributed HBV-96 Hydrological Model.” Journal of Hydrology, 201, 272--288. doi:10.1016/S0022-1694(97)00041-3 .

Maidment DR (1993). Handbook of Hydrology, volume 31. McGraw-Hill Education Ltd. ISBN 0-07-039735-5.

Perrin C, Michel C, Andréassian V (2003). “Improvement of a Parsimonious Model for Streamflow Simulation.” Journal of Hydrology, 279(1-4), 275--289. ISSN 00221694, doi:10.1016/S0022-1694(03)00225-7 .

Quick MC, Pipes A (1977). “U.B.C. WATERSHED MODEL / Le Modèle Du Bassin Versant U.C.B.” Hydrological Sciences Bulletin, 22(1), 153--161. ISSN 0303-6936, doi:10.1080/02626667709491701 .

Wood EF, Lettenmaier DP, Zartarian VG (1992). “A Land-Surface Hydrology Parameterization with Subgrid Variability for General Circulation Models.” Journal of Geophysical Research, 97(D3), 2717. ISSN 0148-0227.

Zhao R (1992). “The Xinanjiang Model Applied in China.” Journal of Hydrology, 135(1), 371--381. ISSN 0022-1694, doi:10.1016/0022-1694(92)90096-E .