actuall evapotranspiration

Actual ET, or actual evapotranspiration, is a measure of the amount of water that is lost from the land surface through evaporation and transpiration by plants.

Under the concept of the conceptual HM, the actual ET is always calculated by the potential ET \(E_p\), which evaluates the meteorological and landuse (vegetation) situations. The second point to consider is the water availability of the land or soil.

So we can give the function from:

\[E_a = f_{evatransActual}(D_{atms}, D_{lssg})\]

to:

\[E_a = f_{evatransActual}(E_p, W_{lssg}, ...) = k^* E_p\]

where

• \(E_a\) is land_evatrans_mm or soil_evatrans_mm

• \(E_p\) is atmos_potentialEvatrans_mm

• \(k^*\) is estimated ratio.

Then the different evatransActual methods will estimate the ratio \(k^*\).

The output density distribution from 7 methods:

Usage

evatransActual_SupplyRatio(
  atmos_potentialEvatrans_mm,
  water_mm,
  capacity_mm,
  param_evatrans_sur_k
)

evatransActual_SupplyPow(
  atmos_potentialEvatrans_mm,
  water_mm,
  capacity_mm,
  param_evatrans_sup_k,
  param_evatrans_sup_gamma
)

evatransActual_VIC(
  atmos_potentialEvatrans_mm,
  water_mm,
  capacity_mm,
  param_evatrans_vic_gamma
)

evatransActual_GR4J(atmos_potentialEvatrans_mm, water_mm, capacity_mm)

evatransActual_UBC(
  atmos_potentialEvatrans_mm,
  water_mm,
  capacity_mm,
  param_evatrans_ubc_gamma
)

evatransActual_LiangLand(
  atmos_potentialEvatrans_mm,
  water_mm,
  capacity_mm,
  param_evatrans_lia_gamma
)

evatransActual_LiangSoil(
  atmos_potentialEvatrans_mm,
  water_mm,
  capacity_mm,
  param_evatrans_lia_B
)

Arguments

atmos_potentialEvatrans_mm

(mm/m2/TS) potential / reference evapotranspiration

water_mm

(mm/m2/TS) water volume in soilLy, groundLy or intercept of landLy, same as soil_water_mm, ground_water_mm or land_interceptWater_mm

capacity_mm

(mm/m2) water storage capacity in soilLy, groundLy or intercept of landLy, same as soil_capacity_mm, ground_capacity_mm orland_interceptCapacity_mm

param_evatrans_sur_k

<0.1, 1> parameter for evatransActual_SupplyRatio(), ratio of potential ET, that is estimated as actually ET

param_evatrans_sup_k

<0.1, 1> parameter for evatransActual_SupplyPow(), ratio of this method

param_evatrans_sup_gamma

<1, 5> parameter for evatransActual_SupplyPow(), exponent of this method

param_evatrans_vic_gamma

<0.2, 5> parameter for evatransActual_VIC()

param_evatrans_ubc_gamma

<0.5, 2> parameter for evatransActual_UBC()

param_evatrans_lia_gamma

<0.4, 1> parameter for evatransActual_LiangLand()

param_evatrans_lia_B

<0.01, 3> parameter for evatransActual_LiangSoil()

Value

actually ET in (mm/m2/TS)

• evaporation in interception (landLy), land_evatrans_mm

• transpiration in root

• evaporation in soil (soilLy), soil_evatrans_mm

_SupplyRatio:

The water content (the ratio to the maximal capacity) is considered as th main factors for the ratio \(k^*\). \[k^* = k \frac{W}{C}\] where

• \(W\) is water volume in (mm/m2/TS), water_mm, land_interceptWater_mm, soil_water_mm

• \(C\) is water capacity in (mm/m2), capacity_mm, land_interceptCapacity_mm, soil_capacity_mm

• \(k\) is param_evatrans_sur_k

_SupplyPow:

The water content (the ratio to the maximal capacity) is considered as th main factors for the ratio \(k^*\). \[k^* = k \left(\frac{W}{C}\right)^\gamma\] where

• \(k\) is param_evatrans_sup_k

• \(\gamma\) is param_evatrans_sup_gamma

_VIC (Wood et al. 1992) :

This method is similar with evatransActual_SupplyPow(), estimate the water content in the storage. \[k^* = 1-\left(1-\frac{W}{C}\right)^{\gamma}\] where

• \(\gamma\) is param_evatrans_vic_gamma

_GR4J (Perrin et al. 2003) :

It is a little different than other method, it estimate not the ratio \(f\), rather dieectly a equation with potential ET and water content. And it need no parameter. \[E_a = \frac{W\left(2-\frac{W}{C}\right)\tanh \left(\frac{E_p}{C}\right)}{1 + \left(1-\frac{W}{C}\right)\tanh \left(\frac{E_p}{C}\right)}\]

_UBC (Quick and Pipes 1977) :

It estimates the water content in the storage. (This is a little different than original, the parameter P0AGEN is replaced by \(\frac{C}{\gamma}\).) \[k^* = 10^{\gamma \frac{W-C}{C}}\] where

• \(\gamma\) is param_evatrans_ubc_gamma

_LiangLand (Liang et al. 1994) :

It is also a similar method like evatransActual_SupplyPow(), but it will estimate the supply ability agian, whwn the water is still not enough. \[E_a^* = \left(\frac{W}{C}\right)^\gamma E_p\] \[E_a = \min \left(1, \frac{W}{E_a^*}\right) E_a^*\] where

• \(E_l^*\) is the first estimated actuall ET

• \(E_l\) is actuall ET from land, land_evatrans_mm

• \(\gamma\) is param_evatrans_lia_gamma

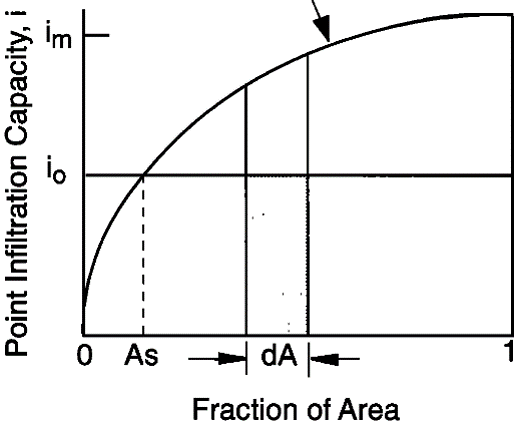
_LiangSoil (Liang et al. 1994) :

It estimates the water content in the storage. (This is a little different than original, the parameter P0AGEN is replaced by \(\frac{C}{\gamma}\).) \[k^* = \int_{0}^{A_{s}} {\rm d} A + \int_{A_{s}}^{1} \frac{i_{0}}{i_{m} [1-(1-A)^{1 / B} ]} {\rm d} A \] where

• \(B\) is param_evatrans_lia_B

• \(A\) is fraction of area

References

Liang X, Lettenmaier D, Wood E, Burges S (1994). “A Simple Hydrologically Based Model of Land Surface Water and Energy Fluxes for GSMs.” J. Geophys. Res., 99. doi:10.1029/94JD00483 .

Perrin C, Michel C, Andréassian V (2003). “Improvement of a Parsimonious Model for Streamflow Simulation.” Journal of Hydrology, 279(1-4), 275--289. ISSN 00221694, doi:10.1016/S0022-1694(03)00225-7 .

Quick MC, Pipes A (1977). “U.B.C. WATERSHED MODEL / Le Modèle Du Bassin Versant U.C.B.” Hydrological Sciences Bulletin, 22(1), 153--161. ISSN 0303-6936, doi:10.1080/02626667709491701 .

Wood EF, Lettenmaier DP, Zartarian VG (1992). “A Land-Surface Hydrology Parameterization with Subgrid Variability for General Circulation Models.” Journal of Geophysical Research, 97(D3), 2717. ISSN 0148-0227.